Minicooper

Bild skapad med Adobe Express.

På Matematikbiennalen 2020 i Växjö lyssnade jag på en föreläsning av Jonas Bergman och Anna Lindgren med rubriken "5-minutare för att öva säkerhet i grundläggande räknefärdigheter och ge ökad självkänsla i matematik". De delade med sig av sina erfarenheter och resultat av ett 1-årigt forskningsprojekt som syftat till att öka de grundläggande räknefärdigheterna och självkänslan i matematik hos elever på gymnasiets yrkesförberedande program. Det var en väldigt inspirerande föreläsning och detta var något som jag direkt tillämpade i min undervisning.

Minicooper är ett övningspapper som eleverna får framför sig under fyra olika tillfällen. De tre första gångerna tas resultatet inte med i bedömningen utan det är först det fjärde och sista som jag noterar. De tre första gångerna är till för att eleven ska kunna se sin egen utveckling och lägga märke till vad hen lär sig medan vi tränar på innehållet. Jag brukar ha ungefär en vecka emellan varje testsituation. Själva namnet "minicooper" kommer ifrån att eleverna har 6 minuter på sig att göra pappret (dvs hälften av vad en cooper är tidsmässigt). Så förutom att träna innehållet tränar vi snabbhet och att vissa uppgifter ska vara mekaniska (då man kan dem). Det är nu fem år sedan jag introducerade denna övning med eleverna. Och idag då jag hade omgång tre med mina nior insåg jag att jag nog skulle behöva byta namnet på övningen till "cooper". Nuförtiden är det nog ingen som klarar uppgifterna på under 6 minuter (jag minns att för fyra år sedan hade jag en klass där flera skrev det på under tre minuter). Idag har eleverna till och med svårt med att hinna bli klara på 12 minuter. Detta beror säkert på flera faktorer, bland annat att eleverna är långsammare i att utföra uppgifter och att kunskapsnivån har sjunkit. 

Ursprungligen hade jag alltid exakt samma övningspapper alla fyra gångerna. Nuförtiden får eleverna ett annat den fjärde och sista gången. Många lärde sig utantill uppgifterna, dvs. då var det inte längre frågan om att kunna lösa dem utan att minnas dem. Dessutom behöver jag inte vara lika orolig för att smygfoton av uppgifterna har spridits bland eleverna. 

Material: Minicooper för potenser och polynom åk 9
Tidsåtgång: 6-12 min

Förhållande med AI

Jag har det senaste året försökt ta åt mig så mycket matnyttigt som möjligt gällande AI. Bland annat fokuserade jag höstens fortbildningar till föreläsningar om AI, så det blev att delta i ett flertal med innehållet hur AI kan användas i undervisningen. Det kan vara att jag antar fel, men jag tror att ganska många lärare låter bli att använda AI med tron att det är som att "fuska". Jag anser (och även föreläsarna jag lyssnade på) att AI är ett verktyg man med gott samvete kan använda för att bland annat spara tid och få idéer.  Jämför att använda AI med att använda en vanlig räknare: Det är bra att kunna huvudräkning, men i något skede är det vettigare att låta en maskin göra arbetet, men du bör ändå kunna validera svaret genom att veta om det är rimligt eller inte. Så länge man kommer ihåg att man som lärare kontrollerar igenom det AI föreslår, anpassar det till sitt egna elevunderlag och tittar på det med "pedagogiska lärarögon" så har vi till vårt förfogande ett verktyg som kan underlätta vårt arbete. Och vad är väl inte bättre än det!!

Här kommer ett övningspapper som jag gjorde åt en av mina klasser nyligen. Det är en klass som behöver anpassat material och som behöver mycket upprepningar av liknande uppgifter. 

Här är prompten jag skrev åt Chat GPT:

"Hej! Kan du skapa 15 övningar åt 14 åringar där de ska öva att beräkna förhållandet mellan två tal? De första 5 övningarna skall vara endast tal, de följande 5 övningarna tal med enheter (alltid samma enhet i båda talen) och till sist 5 uppgifter med värden där enheterna är olika. Vid varje uppgift ska du också fråga efter förhållandets värde. Kan du ge detta i pdf form?"

Inom några sekunder var uppgifterna klara. Jag läste igenom dem, kontrollerade att värdet på förhållandet blev olika (justerade därför några uppgifter) och satt det sedan in i ett dokument åt eleverna. Detta tog inte många minuter, men om jag skulle ha skapat allt från början själv hade det troligtvis tagit tre gånger så lång tid.

Jag hoppas att även DU "vågar" utnyttja AI. Jag hör gärna erfarenheter gällande material som skapats men också om hur eleverna har använt sig av AI (vilket jag också har funderat mycket på på sista tiden). 

Material: Övningspapper 

Multipikationsspel

Detta är ett spel som tränar multiplikation och faktorisering samt befäster begreppen faktor och produkt.  

Spelets gång:
Dela i klassen i grupper på 2 - 4 elever. Den som har det längst förnamnet börjar. En speltur börjar alltid med att man säger en multiplikation vars produkt är talet man står på. Multiplikationen får bestå av fler än två faktorer. Om multiplikationen inte har sagts tidigare, får man kasta tärningen och gå så många steg framåt som ögontalet visar. Sedan är det nästa spelares tur. Om man inte kommer på en multiplikation eller inte kommer på en ny multiplikation (en som inte sagts) tar man ett steg bakåt. Den som kommer först i mål vinner.   

Material: Spelplan, spelpjäser, tärning, anteckningsmaterial
Tidsåtgång: 20 min

Sherlock

Ett av mina favorit datorspel under uppväxten var Sherlock (det andra var Tetris 😀). Det finns att spela fortfarande, men eftersom jag försöker att undvika spel på datorer i klassrummet (antar att de flesta elever gör det helt tillräckligt på fritiden) så skapade jag en pappersvariant av spelet. (Till exempel här kan man spela det online.)

Först lite reklam om själva spelet. Spelet tränar olika förmågor hos eleven:

Logiskt tänkande – Spelet kräver att eleven drar slutsatser baserat på ledtrådar.

Problemlösningsförmåga – Eleven måste analysera den information som finns och hitta den mest effektiva vägen till en lösning.

Känna igen mönster – Eleven behöver kunna identifiera samband mellan olika ledtrådar och använda dessa för att dra slutsatser.

Resonemang – Spelet bygger på att utesluta omöjliga alternativ för att komma fram till den enda möjliga lösningen. 

Koncentration och uthållighet – Att lösa Sherlock-pusslen kräver noggrannhet och uppmärksamhet på detaljer under längre tid.

Minne – Eleven måste hålla reda på tidigare slutsatser och information för att kunna använda dem till att komma vidare i pusslet.

Spelets gång:
Målet är att komma underfund med i vilken kolumn varje person, frukt, hus, fordon, bokstav och tärning ska vara. Överst på pappret står det om man vet färdigt någon position. Till näst kommer kolumn-ledtrådar, dvs. de som är under varandra ska finnas i samma kolumn. Sedan har vi de olika rad-ledtrådarna:

Figurerna finns i kolumnerna bredvid varandra. 

Figurerna finns INTE bredvid varandra. 

Apelsin finns till vänster om röda huset.

Vita huset finns mellan barnet och bokstaven C.
Gäller även i omvänd ordning, dvs. C, vitt hus, barn.
Gäller de tre på varandra följande kolumnerna, 
dvs. inga kolumner emellan. 

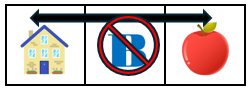Gula huset och äpplet har en kolumn emellan sig
och i den kolumnen får bokstaven B inte finnas.

Ledtrådarna skall läsas igenom flera gånger eftersom man hela tiden får nya tips. Då när eleverna vet var en figur inte kan vara ska de kryssa över den figuren på sin spelplan. Då när eleven vet var en figur kan vara, kan de ringa in den figuren (eller så bestämmer de själva hur de vill markera på sin spelplan). Då när de vet med säkerhet en figurs position placerar de kortet på rätt ställe (använd gärna häftmassa, annars kan de glida omkring på spelplan). Detta är lite knepigare än då man spelar på datorn. Där försvinner de alternativ man klickar bort eller då man placerar med säkerhet en figur på en plats. Så lite råddigare är det nog med pappersversionen, men eleverna tyckte nog att det fungerade riktigt bra ändå. Man måste bara vara noga och konsekvent i sitt markerande på spelplan. 

Varje pussel har endast en lösning (har lagt facit med som sista bild i bilagan). Man ska inte behöva gissa sig fram till något i något skede av spelet. Om man kör fast är det oftast just resonemang man måste ta sig till, dvs. utesluta alternativ baserat på ledtrådarna. 

Jag har låtit eleverna själva välja om de vill jobba i par eller ensamma. Båda har sina fördelar och nackdelar i detta spel. Tre elever i en grupp skulle jag avråda från. 

Tidsåtgång: Beror på elev och pussel, men minst 15 min

Material: Spelplan, uppsättning med de olika figurerna (en figur/kort), vattenlöslig tusch, ledtrådar till pussel. Kopieringsunderlag för sex olika pussel (jag har gjort en uppsättning med 14 spelplaner och påsar med figurerna, så att vissa kan jobba ensamma och vissa i grupp. Själva pusslen kopierar jag bara upp, dvs. dem laminerar jag inte.)